[et_pb_section fb_built=”1″ _builder_version=”4.17.6″ _module_preset=”default” custom_padding=”||8px|||” global_colors_info=”{}”][et_pb_row _builder_version=”4.17.6″ _module_preset=”default” global_colors_info=”{}”][et_pb_column type=”4_4″ _builder_version=”4.17.6″ _module_preset=”default” global_colors_info=”{}”][et_pb_post_title _builder_version=”4.17.6″ _module_preset=”default” title_font=”EB Garamond||||||||” hover_enabled=”0″ global_colors_info=”{}” sticky_enabled=”0″][/et_pb_post_title][et_pb_text _builder_version=”4.17.6″ _module_preset=”default” text_font=”EB Garamond||||||||” text_font_size=”16px” header_font=”EB Garamond||||||||” hover_enabled=”0″ global_colors_info=”{}” header_2_font=”EB Garamond||||||||” sticky_enabled=”0″]

Középiskolás matematika tanulmányaink során fontos tisztában lenni azzal, hogy pontosan mik a számhalmazok. A 9. évfolyam elején tanuljuk (ismételjük át) a halmazok témakörében, de nem csak ott van szükség az ismeretére. Például minden esetben amikor úgy kezdődik egy feladat szövege, hogy oldjuk meg a … számok halmazán a következő feladatot.

• Melyikbe milyen számok tartoznak?
• Melyiknek mi a jele?
• Milyen kapcsolatban vannak egymással?

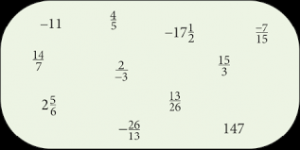
Természetes számok halmaza

A számfogalom fejlődése és a számhalmazok kialakulása az emberiség fejlődésével párhuzamosan ment végbe. A kezdetektől indulva gondoljuk végig, hogyan alakultak ki a jelenleg általunk a mindennapokban használt számok. Vissza a természetbe… Gondoljunk csak bele milyen számok voltak természetesek az ősember számára, milyen számokat használhattak. Képzeljük el azt a helyzetet, hogy az ősember kimegy az általa felállított csapdához és megnézi sikerült-e valamilyen állatot elejtenie. Miután hazamegy mit mondhatott az ősasszonynak az elejtett állatok számáról? Hány mamut lehetett a csapdában? 1 mamut, 2 mamut, 3 mamut stb. Ott az őskorban számukra ezek a számok léteztek úgymond ez volt a természetes a számukra, tehát ezek a természetes számok. Később a 20. század elején kombinatorikai megfontolásokból a nullát is ide sorolták.

Egész számok halmaza

Ez az amit mindenki tud. A pozitív egészek, a negatív egészek és a 0. Ez volt a számok evolúciójának 2. lépcsőfoka, megjelentek a negatív számok. Ha valaki kapott 3 aranyat kölcsönbe, majd azt is elköltötte és semmilye nem maradt, akkor az ő vagyona 3 arany tartozás volt, azaz -3 arany. Nos ez már nem természetes, hogy -3 a vagyonunk, de mégis egész.

Racionális számok halmaza

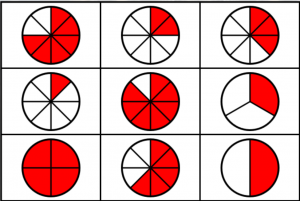
Ha már a fizetős eszköznél vagyunk akkor van abban ráció, hogy azt az aranyat feldaraboljuk valahány részre. Pontosabban a p db aranyat, amit közösen szereztünk elkell osztani q db egyenlő részre. Így mindenkinek p/q arany jut. Az ilyen formában előállítható számokat nevezzük racionálisnak (ésszerűnek). Sőt tovább megyek, minden olyan szám amit egész számok összeadásával, kivonásával, szorzásával, osztásával kapunk az racionális, ésszerű, azaz felfogható. Ezek formailag az egész számok, a véges tizedestörtek és a végelen szakaszos tizedestörtek.

Irracionális számok

Vajon milyen az a szám ami nem ésszerű, nem racionális? Olyan amit egy egész dolog darabolásával nem tudunk megkapni, azaz nem jön ki két egész szám egymással elosztásával. Akkor hogyan tud kijönni? A matematika fejlődésével a négy alapműveleten felül jöttek be más műveletek is, mint pl. a gyökvonás, logaritmus és különböző operátorok, amelyek eredményéül tudtunk kapni ilyen számokat, így keletkeztek az irracionális számok. Ezek formailag a végtelen nem szakaszos tizedestörtek.

Valós számok halmaza

Mivel az előbb említett számok is valamilyen művelet eredménye képpen jöttek ki ezért ezek is valódi számok, tehát valósak csak úgy mint az eddig említett összes többi. Minden a középiskolás tanulmányaink során előforduló szám valós szám.

Melyiknek mi a jele?

Ez viszonylag egyszerűen memorizálható. A jelenkorban már mindenki rendelkezik annyi nyelvtudással, hogy annak segítségével könnyedén megtudja jegyezni.

• Természet=Nature (természetes számok)
• Osztással megkapható számok, Quotient (kvociens) (racionális számok)
• Osztással nem megkapható számok Q* (irracionális számok)
• Valós=Real (valós számok)
• Számok=Zahlen (egész számok) akinek úgy könnyebb, a természetes számok az ellentetjükkel kiegészülve alkotják az egész számok halmazát, mintha a számegyenest átfordítanánk a másik oldalára. Mi meg fordítsuk el az N betűt -> Z.

Ugye nem is olyan nehéz a számhalmazok jeleit és a hozzá tartozó számokat megjegyezni. Az egymáshoz való viszonyukkal kapcsolatban pedig azt kell tudnunk, ha középiskolában egy számra gondolunk, akkor az vagy racionális vagy irracionális. Ha racionális, akkor lehet, hogy tört de lehet, hogy egész. Ha egész akkor lehet, hogy természetes szám, de lehet hogy negatív. Ami biztos, hogy mindenképp valós.

[/et_pb_text][/et_pb_column][/et_pb_row][/et_pb_section]